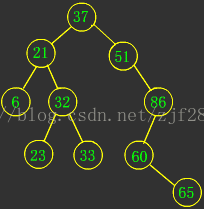
二叉排序树的特征

二叉排序树或者是一棵空树,或者是具有如下特性的二叉树：

    1.每一元素都有一个键值, 而且不允许重复;

    2.若它的左子树不空，则左子树上所有结点的值均小于根结点的值；

    3.若它的右子树不空，则右子树上所有结点的值均大于根结点的值；

    4.它的左、右子树也都分别是二叉排序树。

二叉排序树保存的元素构造

template 
     
      class Element{public:    Element(const Type& _key): key(_key) {}    Element():key(0) {}    Type key;    //在这儿可以很容易的添加更多的数据    //方便对Element进行扩展};
     

二叉排序树节点的设计与实现

template 
     
      class BstNode{    friend class BsTree
      
       ;public:    BstNode(const Element
       
         &_data = 0,            BstNode *_leftChild = NULL,            BstNode *_rightChild = NULL)        : data(_data), leftChild(_leftChild), rightChild(_rightChild) {}    const Type &getData() const    {        return data.key;    }private:    //Node当中保存的是Element元素    Element
        
          data;    BstNode *leftChild;    BstNode *rightChild;    void display(int i);};
        
       
      
     

//中序遍历二叉树://能够保证该二叉树元素按照递增顺序打印出来template 
     
      void BstNode
      
       ::display(int i){    //首先访问左子树    if (leftChild != NULL)        leftChild->display(2*i);    //访问中间节点    //Number表示为如果该树为完全二叉树/满二叉树, 其编号为几    std::cout << "Number: " << i << ", data.key = " << data.key << std::endl;    //访问右子树    if (rightChild != NULL)        rightChild->display(2*i+1);}
      
     

二叉排序树的构造

template 
     
      class BsTree{public://构造与析构    BsTree(BstNode
      
        *init = NULL): root(init) {}    ~BsTree()    {        if (!isEmpty())            makeEmpty(root);    }//二叉查找树的三大主力:插入, 删除, 搜索(又加入了一个迭代搜索)    //插入    bool insert(const Element
       
         &item);    //删除    void remove(const Element
        
          &item)    {        remove(item, root);    }    //递归搜索    const BstNode
         
          * search(const Element
          
            &item) { return search(item, root); } //迭代搜索 const BstNode
           
             *searchByIter(const Element
            
              &item);//实用函数 void display() const { if (root != NULL) root->display(1); } void visit(BstNode
             
               * currentNode) const { std::cout << "data.key = " << currentNode->data.key << std::endl; } bool isEmpty() const { return root == NULL; } void makeEmpty(BstNode
              
                *subTree); //中序遍历 void levelOrder() const;private: const BstNode
               
                * search(const Element
                
                  &item, const BstNode
                 
                   *currentNode); void remove(const Element
                  
                    &item, BstNode
                   
                     *¤tNode);private: BstNode
                    
                      *root;};
                    
                   
                  
                 
                
               
              
             
            
           
          
         
        
       
      
     

二叉排序树的插入算法

    根据动态查找表的定义，“插入”操作在查找不成功时才进行；若二叉排序树为空树，则新插入的结点为新的根结点；否则，新插入的结点必为一个新的叶子结点，其插入位置由查找过程得到。

//二叉排序树插入的实现与解析template 
     
      bool BsTree
      
       ::insert(const Element
       
         &item){    //如果这是新插入的第一个节点    if (root == NULL)    {        root = new BstNode
        
         (item);        root->leftChild = root->rightChild = NULL;        return true;    }    BstNode
         
           *parentNode = NULL;   //需要插入位置的父节点    BstNode
          
            *currentNode = root; //需要插入的位置 while (currentNode != NULL) { //如果二叉树中已经含有了该元素, 则返回插入出错 if (item.key == currentNode->data.key) return false; parentNode = currentNode; //如果要插入的元素大于当前指向的元素 if (item.key < currentNode->data.key) currentNode = currentNode->leftChild; //向左搜索 else currentNode = currentNode->rightChild; //向右搜索 } //此时已经查找到了一个比较合适的插入位置了 if (item.key < parentNode->data.key) parentNode->leftChild = new BstNode
           
            (item); else parentNode->rightChild = new BstNode
            
             (item); return true;}
            
           
          
         
        
       
      
     

二叉排序树的查找算法

若二叉排序树为空，则查找不成功；否则:

    1.若给定值等于根结点的关键字，则查找成功；

    2.若给定值小于根结点的关键字，则继续在左子树上进行查找；

    3.若给定值大于根结点的关键字，则继续在右子树上进行查找。

//二叉排序树搜索的设计与实现//递归搜索template 
     
      const BstNode
      
       * BsTree
       
        ::search(const Element
        
          &item,        const BstNode
         
           *currentNode){    if (currentNode == NULL)        return NULL;    if (currentNode->data.key == item.key)        return currentNode;    if (item.key < currentNode->data.key)        return search(item, currentNode->leftChild);    else        return search(item, currentNode->rightChild);}
         
        
       
      
     

//迭代搜索template 
     
      const BstNode
      
        *BsTree
       
        ::searchByIter(const Element
        
          &item){    for (BstNode
         
           *searchNode = root;            searchNode != NULL;            /*empty*/)    {        if (item.key == searchNode->data.key)            return searchNode;        if (item.key < searchNode->data.key)            searchNode = searchNode->leftChild;        else            searchNode = searchNode->rightChild;    }    return NULL;}
         
        
       
      
     

二叉排序树的删除算法

    和插入相反，删除在查找成功之后进行，并且要求在删除二叉排序树上某个结点之后，仍然保持二叉排序树的特性。

 

删除分三种情况:

    1.被删除的结点是叶子节点:其双亲结点中相应指针域的值改为“空”, 并将该节点删除;

    2.被删除的结点只有左子树或者只有右子树:其双亲结点的相应指针域的值改为 “指向被删除结点的左子树或右子树”, 然后删除该节点;

    3.被删除的结点既有左子树，也有右子树:以其前驱替代之，然后再删除该前驱结点;

//二叉排序树节点删除的实现与解析如下template 
     
      void BsTree
      
       ::remove(const Element
       
         &item,                          BstNode
        
          *¤tNode){    if (currentNode != NULL)    {        //如果要删除的元素小于当前元素        if (item.key < currentNode->data.key)            remove(item, currentNode->leftChild);   //向左搜索删除        //如果要删除的元素大于当前元素        else if (item.key > currentNode->data.key)            remove(item, currentNode->rightChild);  //向右搜索删除        //如果要删除掉的元素等于当前元素(找到要删除的元素了)        // 并且当前节点的左右子女节点都不为空        else if ((currentNode->leftChild != NULL) && (currentNode->rightChild != NULL))        {            //从当前节点的右子女节点开始,            //不断向左寻找, 找到从当前节点开始中序遍历的第一个节点            //找到的这一个节点是在当前子树中, 大于要删除的节点的第一个节点            BstNode
         
           *tmp = currentNode->rightChild;            while (tmp->leftChild != NULL)                tmp = tmp->leftChild;            //用搜索到的节点值覆盖要删除的节点值            currentNode->data.key = tmp->data.key;            //删除搜索到的节点            remove(currentNode->data, currentNode->rightChild);        }        //如果当前节点就是要删除的节点        //并且其左子女(和/或)右子女为空        //默认包含了左右子女同时为空的情况:        //即: 在if中肯定为true        else        {            BstNode
          
            *tmp = currentNode; //如果左子女为空 if (currentNode->leftChild == NULL) //则用他的右子女节点顶替他的位置 currentNode = currentNode->rightChild; //如果右子女为空 else //则用他的左子女节点顶替他的位置 currentNode = currentNode->leftChild; //释放节点 delete tmp; } }}
          
         
        
       
      
     

二叉查找树的几个实用操作

//清空二叉树template 
     
      void BsTree
      
       ::makeEmpty(BstNode
       
         *subTree){    if (subTree != NULL)    {        if (subTree->leftChild != NULL)            makeEmpty(subTree->leftChild);        if (subTree->rightChild != NULL)            makeEmpty(subTree->rightChild);        delete subTree;    }}
       
      
     

//二叉查找树的层次遍历template 
     
      void BsTree
      
       ::levelOrder() const{    std::queue< BstNode
       
         * > queue;    queue.push(root);    while (!queue.empty())    {        BstNode
        
          *currentNode = queue.front();        queue.pop();        visit(currentNode);        if (currentNode->leftChild != NULL)            queue.push(currentNode->leftChild);        if (currentNode->rightChild != NULL)            queue.push(currentNode->rightChild);    }}
        
       
      
     

二叉排序树的性能分析

     对于每一棵特定的二叉排序树，均可按照平均查找长度的定义来求它的 ASL 值，显然，由值相同的 n 个关键字，构造所得的不同形态的各棵二叉排序树的平均查找长度的值不同，甚至可能差别很大(如果二叉查找树退化成一条链表, 则其插入/删除/查找的性能都会退化为O(N))。

     但是在随机情况下, 二叉排序树的搜索, 插入, 删除操作的平均时间代价为O(logN);